이동 평균 종류 및 python 구현
- 목차
0. 데이터
https://www.kaggle.com/datasets/dougcresswell/daily-total-female-births-in-california-1959

1. 단순 이동 평균(Simple Moving Average, SMA)
list = [a0, a1, a2, a3, a4, a5]
window = 3
==> [avg([a0, a1, a2]), avg([a1, a2, a3]), avg([a2, a3, a4]), avg([a3, a4, a5])]def SMA(array, window):
array = np.array(array)
assert array.ndim == 1, "1차원 array만 입력할 수 있습니다."
n = len(array)
result = np.empty(n)
result[:] = np.nan
ma = []
# 0부터 n-window까지
for i in range(0, n-window+1):
m = np.mean(array[i:i+window])
ma.append(m)
result[window-1:] = ma
return np.array(result)
window = 10
sma = SMA(timestamp, window)
# 또는 pandas로
sma = timestamp.rolling(window=window).mean()

2. 누적 이동 평균(Cumulative Moving Average, CMA)
list = [a0, a1, a2, a3, a4, a5]
==> [avg([a0]), avg([a0, a1]), avg([a0, a1, a2]), avg([a0, a1, a2, a3]), ..., avg([a0, a1, a2, a3, a4, a5])]def CMA(array):
array = np.array(array)
assert array.ndim == 1, "1차원 array만 입력할 수 있습니다."
n = len(array)
result = []
for i in range(n):
m = np.mean(array[0:i+1])
result.append(m)
return np.array(result)
3. (선형)가중이동평균(Weighted Moving Average, WMA)
list = [a0, a1, ..., an]
window = m
A = dot product([m, m-1, ..., 1], [ai, a(i-1), ..., a(i-m+1)])
B = m + (m-1) + ... + 1
ma_i = A / Bdef WMA(array, window):
array = np.array(array)
assert array.ndim == 1, "1차원 array만 입력할 수 있습니다."
n = len(array)
result = np.empty(n)
result[:] = np.nan
weight = np.arange(1, window+1, 1)
ma = []
# 0부터 n-window까지
for i in range(0, n-window+1):
A = np.sum(weight * array[i:i+window])
B = np.sum(weight)
m = A / B
ma.append(m)
result[window-1:] = ma
return np.array(result)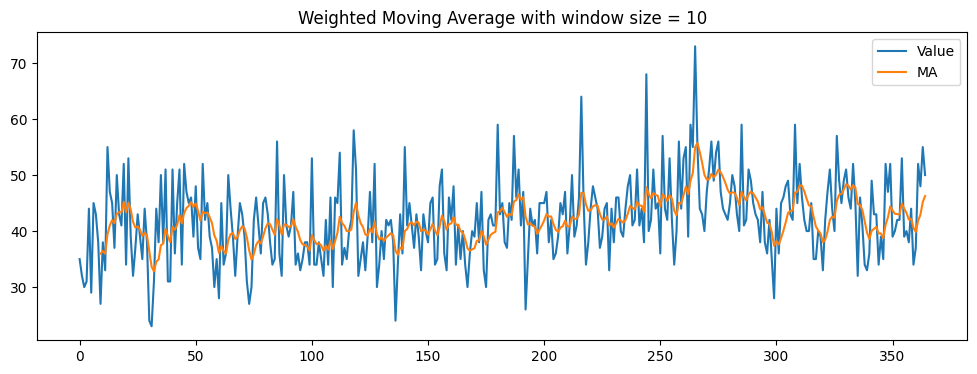
4. 지수가중이동평균(Exponentially Weighted Moving Average, EWMA)
list = [a0, a1, ..., an]
window = m
A = dot product([1, (1-α), (1-α)^2, ..., (1-α)^(m-1)], [ai, a(i-1), ..., a(i-m+1)])
B = 1 + (1-α) + ... + (1-α)^(m-1)
ma_i = A / B$
\begin{multline}
\begin{split}
y_t &= \frac{x_t + (1-\alpha)x_{t-1}+(1-\alpha)^2x_{t-2}+...} {\frac {1}{1-(1-\alpha)}} \\
&= [x_t + (1-\alpha)x_{t-1} + (1-\alpha)^2x_{t-2} + ...]\alpha \\
&= \alpha x_t + [(1-\alpha)x_{t-1}+ (1-\alpha)^2x_{t-2} + ...]\alpha \\
&= \alpha x_t + (1-\alpha)[x_{t-1}+ (1-\alpha)x_{t-2} + ...]\alpha \\
&= \alpha x_t + (1-\alpha)y_{t-1}
\end{split}
\end{multline}
$
⇒ 재귀적으로 활용 가능
$ y_t$는 근사적으로 $\frac {1}{1-\alpha}$만큼의 데이터를 사용해 평균을 구하는 것과 같다고 함.
예) α=0.98 ==> 50개의 데이터 이용 // α=0.9 ==> 10개의 데이터 이용
# 재귀적 계산법
def EWMA(array, alpha):
array = np.array(array)
assert array.ndim == 1, "1차원 array만 입력할 수 있습니다."
n = len(array)
window = int(1/(1-alpha))
weight = np.array([(1-alpha)**i for i in range(0, window)])[::-1]
ma = []
# i == 0일 때
ma.append(array[0])
# 1부터 n-1까지
for i in range(1, n):
m = alpha * array[i] + (1-alpha) * ma[-1] # alpha * x_i + (1-alpha) * y_(t-1)
ma.append(m)
return np.array(ma)
alpha = 0.5
ewma = EWMA(timestamp, alpha)
# 또는 pandas로
ewma = timestamp.ewm(adjust=False, alpha=alpha).mean()pandas 이용 시, `adjust=False`는 재귀적 계산, `adjust=True`는 직접 수식에 의한 계산으로 약간 값의 차이가 있다
| `adjust=False`일 때 | `adjust=True`일 때 |
 |
 |

전체 코드
참조
'데이터 분석' 카테고리의 다른 글
| WSL Ubuntu에서 Vue.js 앱을 로컬호스트로 올리고 코드 수정하기 (0) | 2025.03.17 |
|---|---|
| Granger 인과관계 (0) | 2025.03.12 |
| Windows에서 WSL2와 Ubuntu 설치 및 Docker 사용하기 (0) | 2025.02.28 |
