머신러닝으로 야구 득/실점 예측해보기 (5) 머신러닝
- 목차
나의 머신러닝 지식은 매우매우 초보단계다. 지금도 공부 중이다.
그러니 이 방법이 제일(그나마) 정확하다고 하기 힘들다.
그냥 재미로 봐주길 바란다.
scikit learn 사이트에 어떤 머신러닝을 이용하면 좋은지 알려주는 맵이 있다.
https://scikit-learn.org/stable/tutorial/machine_learning_map/
Choosing the right estimator — scikit-learn 0.22.2 documentation
Choosing the right estimator Often the hardest part of solving a machine learning problem can be finding the right estimator for the job. Different estimators are better suited for different types of data and different problems. The flowchart below is desi
scikit-learn.org
>50 Samples => YES => predicting a category => NO => predicting a quantity => YES => ...
그러면 regressions로 간다. 소개된 부분을 아는만큼 해봤지만 좋은 결과가 잘 나오지 않았다.
정확도가 기껏해야 20~30% 였다.
그래서 그나마 괜찮았던 방법인 Random Forest로 돌려본 결과를 소개한다.
한 경기의 득/실점이 최근 5경기의 득/실점의 영향을 받는다고 가정했다.
그리고 해가 바뀌면 최근 5경기는 의미가 없다고 보고 그런 경우는 제외했다.
from sklearn.ensemble import RandomForestClassifier
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import os
base_dir = 'C:/Users/Username/Desktop'
excel_file = "lotte.xlsx"
excel_dir = os.path.join(base_dir, excel_file)
df = pd.read_excel(excel_dir, encoding="EUC_KR")
train_year = (df["YEAR"] <= 2018)
test_year = (df["YEAR"] >= 2019)
interval = 5
def make_data(data):
x_r = []
y_r = []
x_er = []
y_er = []
r = list(data["R"])
er = list(data["ER"])
for i in range(len(r)):
if i < interval : continue
elif data.iloc[i, 0] != data.iloc[i-1, 0] : continue
y_r.append(r[i])
y_er.append(er[i])
xa = []
xb = []
for p in range(interval):
d = i + p - interval
xa.append(r[d])
xb.append(er[d])
x_r.append(xa)
x_er.append(xb)
return (x_r, y_r, x_er, y_er)
train_x_r , train_y_r, train_x_er, train_y_er = make_data(df[train_year])
test_x_r, test_y_r, test_x_er, test_y_er = make_data(df[test_year])
model1 = RandomForestClassifier()
model2 = RandomForestClassifier()
model1.fit(train_x_r, train_y_r)
model2.fit(train_x_er, train_y_er)
pre_y_r = model1.predict(test_x_r)
pre_y_er = model2.predict(test_x_er)
diff_y_r = abs(pre_y_r-test_y_r)
diff_y_er = abs(pre_y_er-test_y_er)
a = [x for x in diff_y_r if x <= 2]
b = [x for x in diff_y_er if x <= 2]
print("average_r =", sum(diff_y_r)/len(diff_y_r), "max_r =", max(diff_y_r), "score =", len(a)/len(diff_y_r)*100)
print("average_er =", sum(diff_y_er)/len(diff_y_er), "max_er =", max(diff_y_er), "score =", len(b)/len(diff_y_er)*100)
wdl = []
for i in range(len(pre_y_r)):
if abs(pre_y_r[i]-pre_y_er[i]) == 0 :
wdl.append("무")
elif pre_y_r[i] > pre_y_er[i] :
wdl.append("승")
else :
wdl.append("패")
data = df[test_year]
test_wdl = list(data["WDL"])
y = 0
for i in range(len(wdl)):
if wdl[i] == test_wdl[i]:
y += 1
print("승패 정확도 :", y/len(wdl)*100)
plt.subplot(2, 1, 1)
plt.plot(test_y_r, c='r')
plt.plot(pre_y_r, c='b')
plt.subplot(2,1,2)
plt.plot(test_y_er, c='r')
plt.plot(pre_y_er, c='b')
plt.show()
| average_r = 3.115107913669065 max_r = 13 score = 30.215827338129497 average_er = 3.5467625899280577 max_er = 14 score = 26.618705035971225 승패 정확도 : 48.92086330935252 |
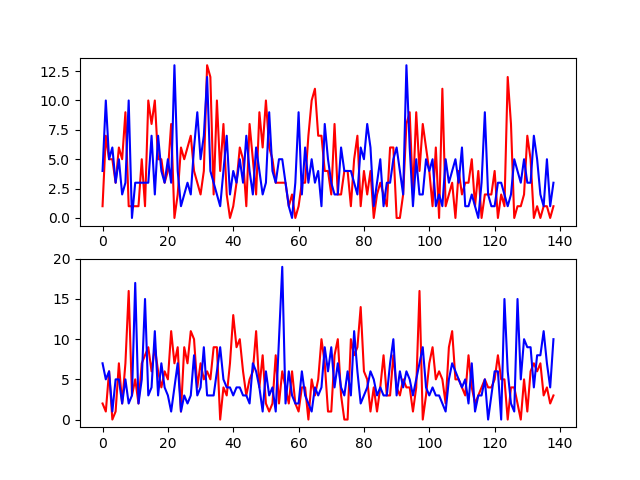
득/실점 정확도가 25~30%로 아주 실망스러운 수준이 나왔다. 그마저도 2점차이로 예상한 것도 정답이라 했을 때인데도...
예측과 실제의 차이의 평균은 3~3.5점, 최대 13, 14점 정도였다.
그래도 승패를 맞춘다면 그건 그거 나름 좋은 결과이므로 그것도 확인해보았으나 49%로 아쉬운 결과가 나왔다.
요일별로도 확인을 해봤지만 정확도는 비슷하거나 더 떨어졌다.
결론은 역시 자연현상이 아닌 것을 예측하는 것은 힘든 일이라는 사실을 확인했다는 것과
머신러닝을 좀 더 배워야겠다는 점이다.
공인구의 영향이나 타고투저, 투고타저 시즌 등 고려사항도 더 있을 것이다.
오히려 자연현상과 연결지어서 온도, 습도별 홈런 수 예측하기 같은 것도 재밌을 것 같다.
하지만 그러려면 더 방대한 데이터가 필요할 것 같다. (구장별 온습도)
아무튼 결과의 좋고 나쁨을 떠나서 좋은 공부가 되었다.
'데이터 분석 > 머신러닝' 카테고리의 다른 글
| 머신러닝과 기상 데이터를 이용해 홈런 갯수 예측해보기 (2) 홈런 데이터 가져오기 (0) | 2020.05.10 |
|---|---|
| 머신러닝과 기상 데이터를 이용해 홈런 갯수 예측해보기 (1) 소스 가져오기 (0) | 2020.05.10 |
| 머신러닝으로 야구 득/실점 예측해보기 (4) 데이터 저장 (0) | 2020.05.05 |
| 머신러닝으로 야구 득/실점 예측해보기 (3) 스코어 뽑아내기 (0) | 2020.05.05 |
| 머신러닝으로 야구 득/실점 예측해보기 (2) string 정리하기 (0) | 2020.05.05 |


