두 개의 분포를 보이는 데이터에 적합한 회귀 모델 만들어보기 (python)
- 목차
1. 상황 가정
회귀 예측 문제를 해결하다 보면 y가 아래와 같은 분포를 가질 때가 있다. 두 종류의 제품이 섞여있는 품질 데이터라던가, 서로 다른 연도에 벌어졌던 리그의 득점 데이터가 그 예가 될 수 있겠다.

이런 상황에서 아래와 같은 가정을 해보았다.
- 중심을 기준으로 데이터를 좌우로 나누는 예측을 해볼 수 있지 않을까?
- 좌우로 나누는데 성공했다면 개별 분포 내에서 회귀 예측을 하면 더 정확하지 않을까?
물론 이건 가정일 뿐, 실제 실험을 해보아야 하며 데이터마다 다른 결과를 낼 수 있다는 점은 유의해야 한다.
2. 모델 만들기
나누는 기준(중심) 부근에서 어떻게 모델을 만들지 두 가지 전략을 정했다.
- 중심 기준으로 정직하게 좌우로 나눠서 좌우를 분류하는 모델과 좌우 각각에서 모델을 만드는 것 (1개 분류 모델과 2개 회귀 모델)
- 중심 근처에서 일정 범위를 벌려서 좌우 각각 분류 모델을 만든 뒤 모델을 만드는 것 (2개 분류 모델과 2개 회귀 모델)

2-1. 두 개의 분류 모델과 두 개의 회귀 모델
중심 근처에서 일정 범위를 벌려서 좌우 각각 분류 모델을 만든 뒤 모델을 만드는 것이라고 했는데, 글로 표현하면 너무 어려우니 그림과 함께 설명을 하고자 한다.

(1) 중심에서 약간 감소한 값을 기준으로 왼쪽, 오른쪽을 구분하는 분류 모델 A와 오른쪽 데이터만으로 회귀 모델 C를 만든다.

(2) 동일한 방법으로 중심에서 약간 증가한 값을 기준으로 왼쪽, 오른쪽을 구분하는 분류 모델 B와 왼쪽 데이터만으로 회귀 모델 D를 만든다.
(3) 예측의 경우 3가지 케이스가 생긴다.
a. 분류 모델 A, B 모두 y가 왼쪽에 있다고 예측하는 경우
→ 왼쪽 회귀 모델 D로 y를 예측한다.
b. 분류 모델 A, B 모두 y가 오른쪽에 있다고 예측하는 경우
→ 오른쪽 회귀 모델 C로 y를 예측한다.
c. 분류 모델 A, B가 서로 y가 다른 곳에 있다고 예측하는 경우
→ 각 분류 모델이 뱉은 확률을 가중치로 삼아 C, D가 각각 예측한 y 값을 가중평균한다.
(A가 왼쪽, B가 오른쪽에 있다고 예측한 경우 왼쪽 회귀 모델 D의 가중치는 A의 확률로, 오른쪽 회귀 모델 C의 가중치는 B의 확률로)

def predict(self, X:pd.DataFrame):
"""
Parameters
----------
X: 테스트 데이터.
Returns
-------
pred: pd.Series. 예측값
"""
# 결과 데이터 초기화
pred = pd.Series([0 for _ in range(len(X))], name=self.label, index=X.index)
# print('예측값 초기화 완료')
# 왼쪽/오른쪽 구간 분류
# 두 개의 분류 모델이 서로 같은 결과를 내놓을 경우
is_left = self.clf_left.predict_proba(X)[:, 0] # 왼쪽 모델의 왼쪽에 대한 확률값
is_right = self.clf_right.predict_proba(X)[:, 0] # 오른쪽 모델의 오른쪽에 대한 확률값
# print('분류 모델 예측 완료')
left_index = (is_left >= 0.5) & (is_right < 0.5)
right_index = (is_left < 0.5) & (is_right >= 0.5)
# 왼쪽/오른쪽 각각 예측
if left_index.sum() > 0:
left = self.reg_left.predict(X[left_index])
pred[left_index] = left
if right_index.sum() > 0:
right = self.reg_right.predict(X[right_index])
pred[right_index] = right
# print('예측값 업데이트 완료')
# 두 개의 분류 모델의 예측 결과가 서로 다른 경우
# 각각의 회귀 모델 예측값의 가중 평균으로 대체, 가중치는 예측 확률값
case1_index = (is_left >= 0.5) & (is_right >= 0.5) # 왼쪽 모델은 왼쪽, 오른쪽 모델은 오른쪽에 있다고 예측한 경우
if len(case1_index) > 0:
case1_left = self.reg_left.predict(X[case1_index])
case1_right = self.reg_right.predict(X[case1_index])
case1_left_weight = is_left[case1_index]
case1_right_weight = is_right[case1_index]
pred[case1_index] = (case1_left * case1_left_weight + case1_right * case1_right_weight) / (case1_left_weight + case1_right_weight)
# print('회귀 모델 Case 1 예측 완료')
case2_index = (is_left < 0.5) & (is_right < 0.5) # 왼쪽 모델은 오른쪽, 오른쪽 모델은 왼쪽에 있다고 예측한 경우
if len(case2_index) > 0:
case2_left = self.reg_left.predict(X[case2_index])
case2_right = self.reg_right.predict(X[case2_index])
case2_right_weight = is_left[case2_index]
case2_left_weight = is_right[case2_index]
pred[case2_index] = (case2_left * case2_left_weight + case2_right * case2_right_weight) / (case2_left_weight + case2_right_weight)
# print('회귀 모델 Case 2 예측 완료')
return pred
2-2. 한 개의 분류 모델과 두 개의 회귀 모델
위처럼 범위를 두지 않고 정직하게 좌우로 나누는 분류 모델 A를 학습하고 왼쪽, 오른쪽 각각에 대한 회귀모델 B, C를 학습한다. 대신 예측할 때 아래와 같은 전략을 잡았다.
- 왼쪽에 속하는지에 대한 분류 예측 확률이 0.48처럼 애매한 경우, B의 예측값 * 0.48 + C의 예측값 * 0.52로 가중평균을 해준다.
- 이 때, 어느 확률 범위까지 가중평균으로 예측값을 계산할지는 입력으로 받는다.

def predict(self, X, alpha_prob=0.1):
"""
Parameters
----------
X: pd.DataFrame. 테스트 데이터.
alpha_prob: 확률이 차이가 alpha_prob 이하인 경우 가중 평균
ex) 오른쪽 구간에 속할 확률이 0.55인 경우 (왼쪽 구간은 0.45이므로 alpha_prob=0.1 이하)
오른쪽 회귀 예측값 * 0.55 + 왼쪽 회귀 예측값 * 0.45
Returns
-------
pred: pd.Series. 예측값
"""
# 결과 데이터 초기화
pred = pd.Series([0 for _ in range(len(X))], name=self.label, index=X.index)
# print('예측값 초기화 완료')
# 왼쪽/오른쪽 구간 분류
# 확률의 차이가 alpha_prob보다 큰 경우
is_left = self.clf.predict_proba(X)[:, 0] # 왼쪽일 확률
# print('분류 모델 예측 완료')
left_index = is_left >= 0.5 + alpha_prob / 2
right_index = is_left < 0.5 - alpha_prob / 2
# 왼쪽/오른쪽 각각 예측
if left_index.sum() > 0:
left = self.reg_left.predict(X[left_index])
pred[left_index] = left
if right_index.sum() > 0:
right = self.reg_right.predict(X[right_index])
pred[right_index] = right
# print('예측값 업데이트 완료')
# 확률의 차이가 alpha_prob 이하일 경우
# 각각의 회귀 모델 예측값의 가중 평균으로 대체
case_index = (is_left < 0.5 + alpha_prob / 2) & (is_left >= 0.5 - alpha_prob / 2)
if len(case_index) > 0:
case_left = self.reg_left.predict(X[case_index])
case_right = self.reg_right.predict(X[case_index])
case_left_weight = is_left[case_index]
case_right_weight = 1-is_left[case_index]
pred[case_index] = (case_left * case_left_weight + case_right * case_right_weight)
# print('회귀 모델 Case 1 예측 완료')
return pred
3. 예제
y가 아래와 같은 분포를 가지는 데이터가 있다.
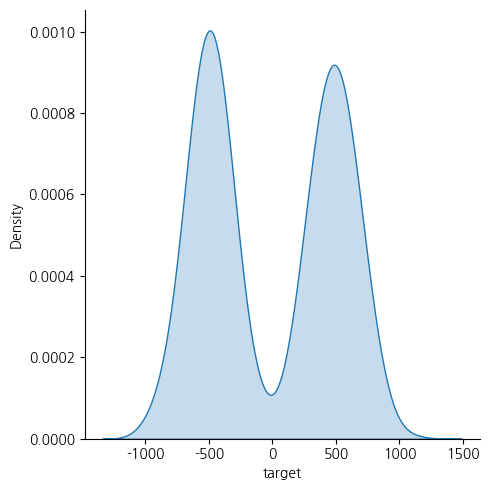
-500과 500 부근에 많은 분포를 가지는 두 종류의 데이터가 섞여있다.
3-1. 하나의 회귀 모델
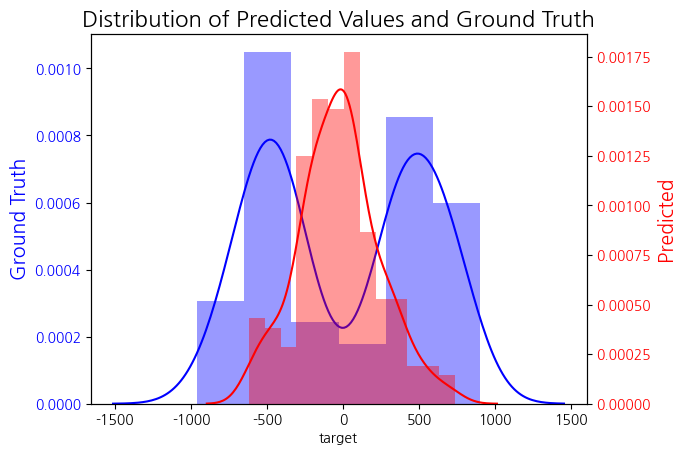
먼저, 위처럼 분류모델을 넣어서 만들어보기 전에 한 개의 회귀모델로 예측해보았다.
MAE=511, RMSE=569로 실제값은 두 개의 분포를 가지는데 반해 예측은 0 부근에서 대부분의 값을 가진다.
3-2. 두 개의 분류 모델과 두 개의 회귀 모델
중심을 0, 범위를 50으로 했을 때 MAE=511, RMS=709로 오히려 예측 결과는 좋지 않았으나 예측값의 분포는 실제와 비슷한 모습을 보였다.
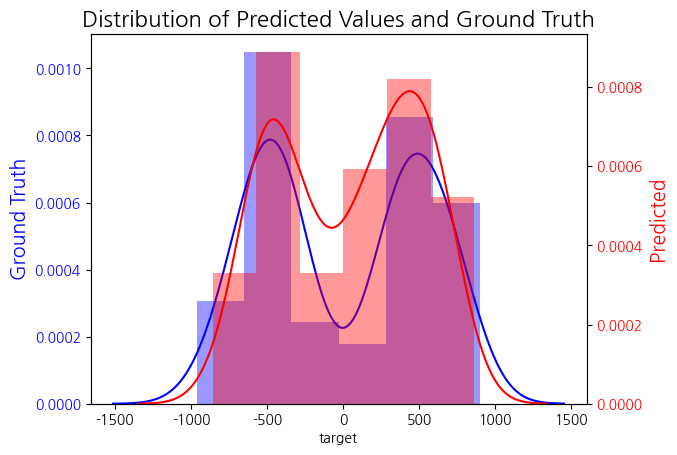
예측 결과가 좋지 않은 이유는 아마 데이터 수가 적은 0 부근에서 많은 예측 값을 가지게 되어서 그런듯하다.
범위를 25로 줄이고 100으로 늘린 결과는 각각 아래와 같다.
| 범위 25 | 범위 100 | |
| MAE | 537 | 547 |
| RMSE | 699 | 696 |
| 이미지 |  |
 |
범위가 커질수록 0 부근 예측값이 많아지는 경향을 보인다.
3-3. 한 개의 분류 모델과 두 개의 회귀 모델
중심을 0, 확률 범위를 0.1로 했을 때 MAE 452, RMSE 645로 MAE는 한 개의 회귀모델보다 좋은 결과를 보였으며 예측값 분포 또한 실제와 비슷한 모습을 보였다.

확률 범위를 0, 0.2로 했을 때의 결과는 아래와 같다.
| 확률 범위 0 | 확률 범위 0.2 | |
| MAE | 474 | 472 |
| RMSE | 682 | 646 |
| 이미지 |  |
 |
예상대로 확률 범위가 커지면 0 부근 예측값이 많아진다. (그런데 예측 오차는 확률 범위가 0일 때보다 오히려 줄어든다.)
4. 결론
이 실험은 scikit-learn의 `make_regression`으로 두 개의 데이터를 섞었을 때의 결과이다. 여기서는 한 개의 분류 모델을 쓴 게 두 개의 분류 모델을 쓴 것보다 좋았으나 한 개의 회귀 모델을 쓴 건 이기지 못했다. 분류 후 예측한다는 시스템이 여기서는 잘 작동하지 않았으나, 실제 데이터에 따라 결과는 많이 달라질 것이다. 가정에서부터 "분류가 잘 된다면"이라는 단서가 붙어있기 때문에, 분류가 되지 않는 데이터라면 이 시스템이 잘 작동하지 않을 것이고, 분류가 잘 되면 그만큼 특징이 다른 데이터 두 개가 섞여있다는 말이기 때문에 회귀도 잘 될 것 같다. 물론, 이 경우마저도 단일 회귀 모델이 더 잘 작동할 수도 있다.
요약하면 "데이터마다 결과는 달라질 가능성이 높으니 실험을 많이 해보세요."
참고로, 이 데이터의 경우 분류 모델의 정확도는 52%였다.
5. 코드
- 모델 코드: github
- 전체 코드: github
'데이터 분석 > 머신러닝' 카테고리의 다른 글
| Regression - IBUG 알고리즘 논문 읽기 (0) | 2024.02.27 |
|---|---|
| 상관 관계의 종류 및 python 코드 구현 (0) | 2024.02.19 |
| MultilabelPredictor 만들어보기 (python) (0) | 2024.02.06 |
| 머신러닝에서의 Estimator와 Predictor의 차이 (0) | 2024.02.01 |
| 머신러닝과 기상 데이터를 이용해 홈런 갯수 예측해보기 (4) 머신러닝 (0) | 2020.05.10 |



