상관 관계의 종류 및 python 코드 구현
- 목차
상관 관계의 의미
두 변수 간에 어떤 관련성이 있는지를 나타내는 것으로 상관 관계가 낮으면 두 변수 간 관련성이 거의 없거나 약하다고 할 수 있다.
예) 수학 성적과 과학 성적의 상관 관계, 수학 성적과 스포츠 경기 시청률의 상관 관계
그러나 상관 관계가 높다고 반드시 인과 관계가 있는 것이 아니다. 다른 제 3의 변수에 의해 영향을 받을 수도 있으며 인과 관계가 모호하기도 하고 우연으로 나타나는 것일 수도 있기 때문에 추가적인 분석이 필요하다.
예) 아이스크림 판매량과 선풍기 판매량의 상관 관계 - “기온”이라는 제 3의 변수가 있음
예) 폭행 사건과 폭력적인 영상물 시청의 상관 관계 - 폭력적인 영상을 시청해서 폭행을 한 건지, 원래 폭력적인 사람이기 때문에 폭력적인 영상물을 많이 본 건지 알 수 없다.
예) 해적의 수와 지구의 평균 기온의 상관 관계 - 해적의 수가 줄어든 것과 지구온난화는 관계가 없다.
예) Spurious Correlations (tylervigen.com)

다만 하고자 하는 것이 설명이 아닌 예측이라면 제 3의 변수가 있는 경우를 사용해도 된다.
예) 설명 - 선풍기 판매량을 늘리기 위해 아이스크림의 판매량을 늘리자 (X)
예) 예측 - 선풍기 판매량을 예측하기 위해 아이스크림의 판매량을 확인하자 (O)
상관 관계의 종류
선형 상관 계수(Pearson)

가장 흔히 쓰이는 상관 관계로, 두 연속형 변수가 선형적으로 얼마나 관계가 있는지 -1~1 사이의 값으로 표현된다. 양의 상관 관계면 한 변수가 증가하면 다른 한 변수도 증가하고, 음의 상관 관계면 한 변수가 감소하면 다른 한 변수도 감소하는 모습을 보인다. 상관 계수의 절댓값이 클 수록 높은 (선형) 관계가 있고, 작을 수록 (선형) 관계가 거의 없다. 또한 두 변수 모두 정규분포를 이룬다는 조건이 만족해야 정확한 결과로 사용할 수 있다.
- X, Y: 연속형 변수

import numpy as np
def PCC(X, Y):
X_bar, Y_bar = np.mean(X), np.mean(Y)
p = np.sum((X-X_bar) * (Y-Y_bar)) / ( np.sqrt(np.sum((X-X_bar)**2)) * np.sqrt(np.sum((Y-Y_bar)**2)))
return p
p = PCC(X, Y)
# 또는 scipy를 이용하여
from scipy.stats import pearsonr
p, _ = pearsonr(X, Y)
스피어만 상관 계수(Spearman)

한 변수가 순서형 변수(등수 등)인 경우, 피어슨 상관 관계보다 더 명확하게 결과를 보여주는 상관 관계다. 두 데이터에 순위를 매긴 후, 순위 데이터를 가지고 선형 상관 계수를 구한 것과 같은 결과를 보여준다.
- d: 매칭되는 데이터의 순위 간 차이
 선형 관계와 스피어만 관계 모두 높은 경우 |
 완벽한 선형은 아니지만 순서는 일치하여 스피어만 관계가 매우 높은 경우 |
 일부 노이즈 데이터로 인해 선형 상관계수가 0.6으로 매우 줄어들었지만, 스피어만 상관계수는 여전히 높다 |
def SCC(X, Y):
from scipy.stats import rankdata
rankX = rankdata(X)
rankY = rankdata(Y)
d2 = (rankX - rankY) ** 2
n = len(X)
rho = 1 - 6 * np.sum(d2) / (n * (n**2-1))
return rho
s = SCC(X, Y)
# 또는 scipy를 이용하여
from scipy.stats import spearmanr
s, _ = spearmanr(X, Y)
# 참고 - 순위 데이터를 만든 후 피어슨 상관계수로 구할 수 있다.
from scipy.stats import rankdata
rankX = rankdata(X)
rankY = rankdata(Y)
s, _ = pearsonr(rankX, rankY)
켄달의 타우(Kenddall's Tau)

두 변수 간의 순서쌍의 일치 여부를 가지고 상관 계수를 계산
- C(concordant pair): 순서쌍이 일치하는 개수
- D(disconcordant pair): 순서쌍이 일치하지 않는 개수
- 예)
# rank
a = [1, 2, 3]
b = [3, 1, 2]
"""
0, 1 ==> a[0] < a[1], b[0] > b[1] ==> D += 1
0, 2 ==> a[0] < a[2], b[0] > b[2] ==> D += 1
1, 2 ==> a[1] < a[2], b[1] < b[2] ==> C += 1
"""
C, D = 1, 2- 참고) `scipy`에서는 tau = (P - Q) / sqrt((P + Q + T) * (P + Q + U)) where P is the number of concordant pairs, Q the number of discordant pairs, T the number of ties only in x, and U the number of ties only in y.라고 정의하고 있다
 |
 |
 |
def KT(X, Y):
from itertools import combinations
comb = combinations(range(len(X)), 2)
C, D = 0, 0
for i, j in comb:
if ((X[i] > X[j]) and (Y[i] > Y[j])) or ((X[i] < X[j]) and (Y[i] < Y[j])):
C += 1
else:
D += 1
return (C-D)/(C+D)
tau = KT(X, Y)
# 또는 scipy를 이용하여
from scipy.stats import kendalltau
tau, _ = kendalltau(X, Y)
최대 정보 상관 계수(MIC; Maximal Information Coefficient)
두 변수 간의 비선형적인 상관 관계를 측정하는 데에 사용되는 지표이다. 두 변수 간의 모든 가능한 함수적인 관계를 고려하여, 가장 적합한 함수적인 관계를 찾아내는 방법을 사용한다. 비선형 관계를 알 수 있기 때문에 유용하지만 한편으로는 계산량이 매우 많아 대용량 데이터에는 사용하기 힘들다는 단점이 있다.
10.4 상호정보량 — 데이터 사이언스 스쿨 (datascienceschool.net)

 |
 |
 |
점이연 상관 계수(Point-biserial)

연속형 변수와 이진형 변수 간의 상관 관계를 측정하는 지표이다.
- X: 연속형 변수, Y: 이진형 변수
- $M_i$: Y의 그룹 $i$의 평균
- $n_i$: Y의 그룹 $i$의 데이터 갯수
- $n$: 전체 데이터 갯수
- $s_n$: X의 표준편차

def PBCC(X, Y):
"""
X: continuous variable
Y: binary variable
"""
X = np.array(X)
Y = np.array(Y)
unique = np.sort(np.unique(Y))
assert len(unique)==2, "Y must be binary variable"
var0 = unique[0]
var0_idx = np.where(Y==var0)
M0 = np.mean(X[var0_idx])
n0 = len(var0_idx)
var1 = unique[1]
var1_idx = np.where(Y==var1)
M1 = np.mean(X[var1_idx])
n1 = len(var1_idx)
sn = np.std(X)
n = n0 + n1
rpb = (M1-M0)/sn * np.sqrt(n1*n0 / (n)**2)
return rpb
pbr = PBCC(X, Y)
# 또는 scipy를 이용하여
from scipy import stats
pbr = stats.mstats.pointbiserialr(Y,X).correlation
파이 계수(Phi Coefficient)
 |
 |
범주형-범주형 변수 사이의 상관 관계를 나타내는 지표다. 머신러닝에서는 이진 모델의 성능을 측정하는데 사용하는 지표(Matthews Correlation Coefficient; MCC)로도 사용한다. (1에 가까울 수록 성능이 좋으며 0이면 성능이 무작위 수준에 가까움, -1이면 반대로 예측됨)
| y=1 | y=0 | |
| x=1 | 4 | 1 |
| x=0 | 1 | 6 |
파이 계수 = 0.657
def MCC(X, Y):
"""
X: actual
Y: prediction
"""
X = np.array(X)
Y = np.array(Y)
uniqueX = list(np.sort(np.unique(X)))
uniqueY = list(np.sort(np.unique(Y)))
assert (uniqueX == [0, 1]) and (uniqueY == [0, 1]), "X and Y must be composed by 0 and 1"
import pandas as pd
df = pd.DataFrame({'X':X, 'Y':Y})
ct = pd.crosstab(index=df['X'], columns=df['Y'])
TP = ct.loc[1, 1]
FN = ct.loc[1, 0]
FP = ct.loc[0, 1]
TN = ct.loc[0, 0]
MCC = (TP*TN - FP*FN) / np.sqrt( (TP+FP)*(TP+FN)*(TN+FP)*(TN+FN) )
return MCC
mcc = MCC(actual, prediction)
# 또는 scikit-learn을 이용하여
from sklearn.metrics import matthews_corrcoef
mcc = matthews_corrcoef(actual, prediction)
이외에도 이연 상관계수, 크래머 V(Cramer's V), 사분상관계수 등이 있다.
상관 계수의 문제점
상관 계수가 낮다고 관계가 없다고 할 수 없다. 다른 변수의 영향(교호 관계) 등이 있을 수 있고, 우리가 생각할 수 있는 선형-비선형 외 다른 관계가 있을 수 있기 때문이다.
예) 9개의 영향 인자(X0, X1, …, X8)와 1개의 목표 인자(Y)가 있다. 선형 상관 관계를 살펴보니 아래와 같았다.
from sklearn.datasets import make_regression
seed = 202375
X, y = make_regression(n_features=9, random_state=seed, n_informative=3)
X2, X3과 Y의 관계는 확실히 높아 보이며 X5는 Y와 관계가 없어 보인다.
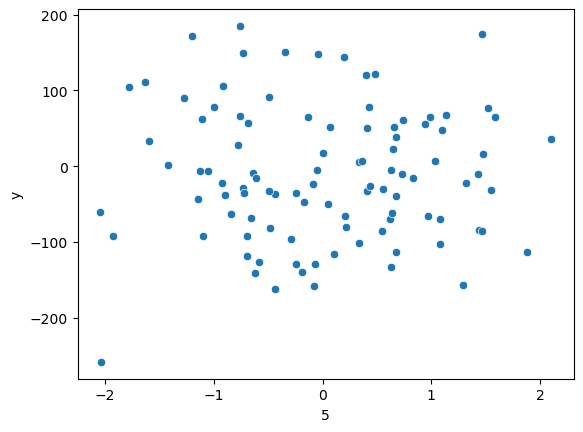
X5와 Y의 관계를 눈으로 확인해도 연관성이 없어 보인다.
하지만 선형 회귀 분석을 했을 때, $Y = 83.358 X2 + 46.849 X3 + 14.529 X5$로, X5가 중요한 인자라는 결과가 나왔다.
즉, 상관 관계가 낮더라도 선형 회귀 분석을 할 때 많은 영향을 줄 수 있기 때문에 데이터 분석 시 주의해서 인자를 고를 필요가 있다.
정리
| 피어슨 상관계수 | 스피어만 상관계수 | 켄달의 타우 | 점이연 상관계수 | 파이 계수 | 최대 정보 상관 계수 | |
| 사용 | 선형 상관관계 | 비선형 상관관계 | 연속형-이진형 변수의 상관관계 | 두 변수간 독립성 파악 | 비선형 상관관계 | |
| 변수 유형 | 연속형-연속형 연속형-순서형 |
연속형-범주형 | 범주형-범주형 | 연속형-연속형 | ||
| 값의 범위 | 1에 가까울 수록 양의 상관 관계 -1에 가까울 수록 음의 상관 관계 0에 가까울 수록 약한 관계 |
1에 가까울 수록 관계가 있음 0에 가까울 수록 관계가 없음 |
||||
| 장점 | 직관적이다 | 데이터 분포 가정이 필요 없다 | ||||
| 단점 | 이상치에 민감하게 반응한다 | 계산량이 많다 | 계산량이 매우 많다 | |||
전체 코드
'데이터 분석 > 머신러닝' 카테고리의 다른 글
| AutoML, Autogluon vs mljar-supervised (0) | 2024.02.29 |
|---|---|
| Regression - IBUG 알고리즘 논문 읽기 (0) | 2024.02.27 |
| 두 개의 분포를 보이는 데이터에 적합한 회귀 모델 만들어보기 (python) (0) | 2024.02.07 |
| MultilabelPredictor 만들어보기 (python) (0) | 2024.02.06 |
| 머신러닝에서의 Estimator와 Predictor의 차이 (0) | 2024.02.01 |



