이상탐지 알고리즘 - ECOD 논문 읽기
- 목차
1. INTRODUCTION
- OD = Outlier Detection
- 기존 OD의 문제점
- 차원의 저주 때문에 정확도와 탐색 시간이 나쁜 영향을 받는다.
- 비지도학습의 하이퍼 파라미터 튜닝의 어려움
- ECOD = Empirical Cumulative distribution functins for Outlier Detection = 이상치 탐색을 위한 경험적 누적 분포 함수
- 희귀한 이벤트(rare events)를 잡아내는 것이 목적
- 가우시안 분포의 꼬리(tail)를 생각할 수 있음 (기존 - "three-sigma" 또는 "1.5 IQR")
- ECDF = Empirical Cumulative Distribution Function
- 파라미터 튜닝 작업이 없음
- 분포에 대해 어떠한 가정도 하지 않음
- 고차원 문제를 단일변수마다 계산하는 것으로 극복, 데이터의 이상함(outlyingness)을 확인
1. 각 변수가 독립이라는 가정을 하고 단일 값이 꼬리에 위치할 확률을 계산
2. 이후 모두를 곱함
- 각 변수가 독립이라고 가정했음에도 잘 작동함
- 장점
- 효과적(Effectiveness)
- 11개의 다른 이상치 탐색 방법들보다 뛰어남
- 효율적이며 확장성 있음(Efficiency and scalability)
- 시간 복잡도가 $ \mathcal{O}(nd)$로 1차원
- $n$: 데이터 포인트 개수, $d$: 차원
- 싱글 스레드, 100만개 데이터, 1만개 피처 이상치 탐색 결과 2시간 걸림
- 하이퍼 파라미터 튜닝 작업이 없기 때문에 시간을 아낄 수 있음
- 해석 가능함(Interpretability)
- 각 데이터가 꼬리에 위치할 확률을 볼 수 있으며 이것을 이상치 점수로 사용할 수 있음
2. RELATED WORK
- 11개의 기존 알고리즘 소개
2-1. Proximity-based Algorithms
- 밀도 기반 또는 거리 기반 알고리즘
- 밀도 기반: 정상 데이터(non-outliers 또는 inliers)가 높은 밀도를 가지는 곳에 위치하는 반면 이상치는 낮은 밀도 지역에 위치함
- LOF(Local Outlier Factor)
- COF(Connective-based Outlier Factor)
- LOCI(LOcal Correlation Integral)
- 거리 기반: 이상치는 다른 데이터들보다 더 멀리 떨어져 있는 데이터
- KNN(k nearest neighbors)
- 모수 분포에 대해 어떠한 가정을 하지 않아 직관적이고 이해하기 쉽다.
- 그러나 계산 복잡도가 높고 하이퍼 파라미터에 민감하다는 단점이 있다.
2-2. Statistical Models
- 모수적 방법: 모수의 분포를 가정함 (GMM(Gaussian mixture models) 등)
- 비모수적 방법: 모수의 분포를 가정하지 않음(KDE(Kernel Density Estimation), HBOS(histogram-based mothods) 등)
- 모수적 방법은 모수 분포를 가정해야한다는 단점이 있고, 비모수적 방법은 게산이 복잡하다는 단점이 있음
2-3. Learning-based Models
- 정상 / 비정상 데이터를 분류 학습
- OCSVM(one-class SVM)
- GANs(generative adversarial networks)
- autoencoders
- reinforcement learning
- 큰 데이터셋에 잘 작동하지만 계산 비용이 비싸며 하이퍼 파라미터 튜닝을 해야 함
- 해석이 어렵다
2-4. Ensemble-based models
- featrue bagging (sub-feature 공간에서 OD 작업)
- isolation forest
- LSCP (개별 포인트마다 다른 estimator를 고름)
- SUOD (많은 heterogeneous estimators를 사용)
- 보다 정확하지만 건들 수 없는 파라미터들이 존재하며 해석하기 어렵다.
3. PROPOSED ALGORITHM: ECOD
3-1. Problem Formulation and Challenges
- 기본 가정
- $n$개의 데이터가 i.i.d 하게 샘플
- $X_1, X_2, ..., X_n \in \mathbb{R}^n$
- 전체 데이터셋 $\mathrm{X} \in \mathbb{R}^{n\times d}$
- $M$: OD 모델
- 각 데이터 $X_i$에 대해 이상치 점수 $O_i \in \mathbb{R}$
- 비지도학습 이상치 탐색의 어려움
- 차원의 저주(Curse of dimensionality): 데이터 수가 많아지거나 차원의 수가 높아지면 정확도가 떨어질 뿐만 아니라 계산 비용이 비싸짐(특히 proximity-based methods)
- 해석의 한계(Limited interpretability): "왜" 이상치인지에 대한 답이 어려움 (fraud detection 등은 그 이유를 요구함)
- 하이퍼파라미터 튜닝의 복잡함(Complexity in hyperparameter tuning)
3-2. The Proposed ECOD
Motivation and High-level Idea
- 이상치는 희귀한 이벤트일 것이며, 이는 확률 분포의 낮은 구간에 위치할 것이다.
- 분포가 unimodal하다면 꼬리에 위치할 것이다.
- 위의 모티베이션에 따라 각 $X_i$마다 ECOD는 "극한(extreme)"일 확률을 계산
- Let $F : \mathbb{R}^d \to [0, 1]$ be joint CDF(cumulative distribution function)
- $X_i$의 $j$번째 피처를 $X_i^{(j)}$라고 하고 $X$를 $X_i$와 동일한 분포를 가지는 랜덤한 변수라고 했을 때
- $F(x) = \mathbb{P} \left( X^{(1)} \le x^{(1)}, X^{(2)} \le x^{(2)}, ..., X^{(d)} \le x^{(d)} \right)$ for any $x \in \mathbb{R}^d$
- $F(X_i)$가 작을 수록 랜덤하게 뽑은 $X$에 대해 부등식 $X \le X_i$이 만족할 확률이 낮아짐
- 그러므로 $F_{\mathrm{X}}(X_i)$ 또는 $1-F_{\mathrm{X}}(X_i)$가 작을 수록 이상치일 확률이 높음
챌린지는 실제 joint CDF를 모르기 때문에 데이터로부터 추정해야한다는 점인데 모든 피처가 독립이라는 가정 하에 수행한다.
- $F(x) = \prod \limits _{j=1}^ d F^{(j)} \left( x^{(j)} \right)$ for $x \in \mathbb{R}^d$
단일 변수 CDF는 경험적 CDF를 사용함으로써 정확히 추정됨을 보일 수 있다.
- $\hat{F}_{\text{left}}^{(j)}(z) := \frac{1}{n} \sum \limits_{i=1}^n \mathbb{1} \{ X_i^{(j)} \le z \}$ for $z \in \mathbb{R}$ where $\mathbb{1} \{\cdot\}$은 indicator function으로, argument가 참이면 1, 아니면 0을 반환하는 함수
- $\hat{F}_{\text{right}}^{(j)}(z):= \frac{1}{n} \sum \limits_{i=1}^n \mathbb{1} \{ X_i^{(j)} \ge z \}$ for $z \in \mathbb{R}$
그러므로 모든 $d$차원에 대한 joint 왼쪽/오른쪽 꼬리 ECDF를 독립 가정 하에서 추정할 수 있다.
- $\hat{F}_{\text{left}}(x) = \prod \limits _{j=1}^ d \hat{F}_{\text{left}}^{(j)} \left( x^{(j)} \right)$ and $\hat{F}_{\text{right}}(x) = \prod \limits _{j=1}^ d \hat{F}_{\text{right}}^{(j)} \left( x^{(j)} \right)$ for $x \in \mathbb{R}^d$
Algorithm 1 Unsupervised OD Using ECDF (ECOD)
Inputs: $\mathrm{X} = \{ X_i \}^n_{i=1} \in \mathbb{R}^{n \times d}$
Outputs: $\mathrm{O} := \text{ECOD} (\mathrm{X}) \in \mathbb{R}^n$
1. for each dimension $j$ in 1, ..., $d$ do
2. 왼쪽, 오른쪽 꼬리 ECDF를 추정
- 왼쪽 꼬리 ECDF: $\hat{F}_{\text{left}}^{(j)}(z)= \frac{1}{n} \sum \limits_{i=1}^n \mathbb{1} \{ X_i^{(j)} \le z \}$ for $z \in \mathbb{R}$
- 오른쪽 꼬리 ECDF : $\hat{F}_{\text{right}}^{(j)}(z)= \frac{1}{n} \sum \limits_{i=1}^n \mathbb{1} \{ X_i^{(j)} \ge z \}$ for $z \in \mathbb{R}$
3. $j$번째 피처 분포의 표본 비대칭도를 계산
- $\gamma_j=\frac{\frac{1}{n}\sum_{i=1}^n \left(X_i^{(j)} - \overline{X^{(j)}} \right)^3}{ \left[ \frac{1}{n-1} \sum_{i=1}^n \left( X_i^{(j)} - \overline{X^{(j)}} \right)^2 \right]^{3/2}}$ where $\overline{X^{(j)}}=\frac{1}{n}\sum_{i=1}^nX_i^{(j)}$
4. end for
5. for 각 표본 $i$ in 1, ..., $n$ do
6. 이상치 점수 $\mathrm{O}_i$를 얻기 위해 $X_i$의 꼬리 확률을 모은다.
- $O_{\text{left-only}}(X_i)=-\sum \limits_{j=1}^d \log {\left( \hat{F}_{\text{left}}^{(j)}(X_i^{(j)}) \right)}$
- $O_{\text{right-only}}(X_i)=-\sum \limits_{j=1}^d \log {\left( \hat{F}_{\text{right}}^{(j)}(X_i^{(j)}) \right)}$
- $O_{\text{auto}}(X_i)=-\sum \limits_{j=1}^d \left[ \mathbb{1} \left\{\gamma_j < 0 \right\} \log {\left( \hat{F}_{\text{left}}^{(j)} \left(X_i^{(j)} \right) \right)} + \mathbb{1} \left\{ \gamma_j \ge 0 \right\} \log { \left( \hat{F}_{\text{right}}^{(j)} \left(X_i^{(j)} \right) \right)} \right]$
7. 최종 이상치 점수를 확정짓는다.
- $O_i = \max \left\{O_{\text{left-only}}(X_i),O_{\text{right-only}}(X_i), O_{\text{auto}}(X_i) \right\}$
8. end for
9. Return 이상치 점수 $\mathrm{O}=(O_1, ..., O_n)$
Aggregating Outlier Scores

- 비대칭도를 써 왼쪽/오른쪽 꼬리 확률을 쓸 지 말 지를 결정함
- 값이 크면 클수록 이상치
4. `pyod`
- https://pyod.readthedocs.io/en/latest/pyod.html
- 지원하는 알고리즘 목록
- ABOD
- ALAD
- AnoGAN
- AutoEncoder
- CBLOF
- COF
- CD
- CDPOD
- DeepSVDD
- ECOD
- FeatureBagging
- GMM
- HBOS
- IForest
- INNE
- KDE
- KNN
- LMDD
- LODA
- LOF
- LOCI
- LUNAR
- LSCP
- MAD
- MCD
- MO_GAAL
- OCSVM
- PCA
- RGraph
- ROD
- Sampling
- SOD
- SO_GAAL
- SOS
- SUOD
- VAE
- XGBOD
# https://github.com/yzhao062/pyod/blob/master/examples/ecod_example.py
from pyod.models.ecod import ECOD
from pyod.utils.data import generate_data
from pyod.utils.data import evaluate_print
from pyod.utils.example import visualize
if __name__ == "__main__":
contamination = 0.1 # percentage of outliers
n_train = 200 # number of training points
n_test = 100 # number of testing points
# Generate sample data
X_train, X_test, y_train, y_test = \
generate_data(n_train=n_train,
n_test=n_test,
n_features=2,
contamination=contamination,
random_state=42)
# train ECOD detector
clf_name = 'ECOD'
clf = ECOD()
# you could try parallel version as well.
# clf = ECOD(n_jobs=2)
clf.fit(X_train)
# get the prediction labels and outlier scores of the training data
y_train_pred = clf.labels_ # binary labels (0: inliers, 1: outliers)
y_train_scores = clf.decision_scores_ # raw outlier scores
# get the prediction on the test data
y_test_pred = clf.predict(X_test) # outlier labels (0 or 1)
y_test_scores = clf.decision_function(X_test) # outlier scores
# evaluate and print the results
print("\nOn Training Data:")
evaluate_print(clf_name, y_train, y_train_scores)
print("\nOn Test Data:")
evaluate_print(clf_name, y_test, y_test_scores)
# visualize the results
visualize(clf_name, X_train, y_train, X_test, y_test, y_train_pred,
y_test_pred, show_figure=True, save_figure=False)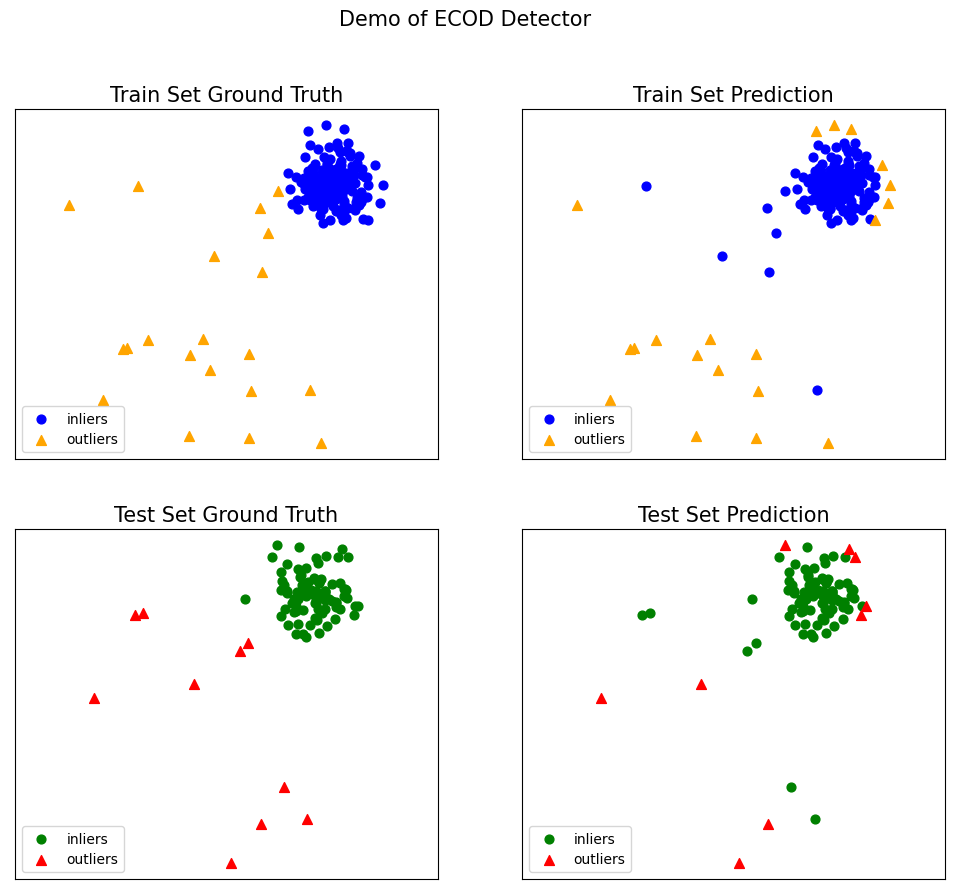
'데이터 분석 > 이상탐지' 카테고리의 다른 글
| 시계열 이상탐지 (4) - 딥러닝의 시대 (0) | 2024.03.25 |
|---|---|
| 시계열 이상탐지 (3) - VAE, TadGAN (0) | 2024.03.22 |
| 시계열 이상탐지 (2) - LSTM-DT, LSTM-AE, AER (0) | 2024.03.20 |
| 시계열 이상탐지 (1) 배경 지식 (0) | 2024.03.15 |



