Fibonacci Search 설명 (python 구현)
- 목차
반응형
Fibonacci Search
함수 $f(x)$가 최소가 되게 하는 $x$를 찾는 알고리즘
수식
0. 피보나치 수열 N개를 만든다.
1. 최소값이 포함된 구간 $[a, b]$를 잡는다.
2. 양 끝점에 대해 $x_1=a+\frac{F_{N-2}}{F_N}L$, $x_2=b-\frac{F_{N-2}}{F_N}L$를 계산한다.
- $L=b-a$
3. 최소값이 존재하지 않는 구간을 제거한다.
- 만약 $f(x_1)<f(x_2)$이면 $b=x_2$, 아니면 $a=x_1$
4. $N=2$가 될 때까지 반복
장단점
- N을 어떻게 잡느냐에 따라 수렴 속도가 달라진다.
구현 소스 코드
class fibonacci_search:
def __init__(self, func, a, b, N=50):
self.func = func
self.a = a
self.b = b
self.N = N
def solve(self):
a_history = [self.a]
b_history = [self.b]
def fibonacci(N):
result = [1, 1]
for i in range(2, N+1):
fi = result[i-1] + result[i-2]
result.append(fi)
return result
fi = fibonacci(self.N)
M = self.N
while M > 2:
L = self.b - self.a
x1 = self.a + fi[M-3] / fi[M-1] * L
x2 = self.b - fi[M-3] / fi[M-1] * L
if self.func(x1) < self.func(x2):
self.b = x2
else:
self.a = x1
a_history.append(self.a)
b_history.append(self.b)
M -= 1
self.minimum = (self.a + self.b) / 2
self.history = [(a, b) for (a, b) in zip(a_history, b_history)]
return self.minimum
예제
$f(x) = \sin ({ \cos ({ \rm{e}^x }) })$
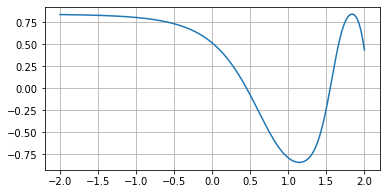
FS = fibonacci_search(a=0, b=1.5, func=f, N=20)
FS.solve() # 1.1449002217294901
f(FS.minimum) # -0.8414709074342859
$g(x) = x^2 + 1$
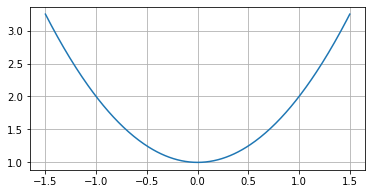
FS = fibonacci_search(a=-1, b=1, func=g, N=50)
FS.solve() # 1.048761945709043e-08
g(FS.minimum) # 1.0
전체 소스 코드 → github
728x90
반응형
'데이터 분석 > 최적화 알고리즘' 카테고리의 다른 글
| 수치 최적화 알고리즘 정리 (0) | 2024.02.02 |
|---|---|
| Lagrange Polynomial Interpolation 설명 (python 구현) (0) | 2024.02.02 |
| Newton's Method (Quadratic interpolation with 2nd derivative) 설명 (python 구현) (0) | 2024.02.02 |
| Golden Section Search 설명 (python 구현) (0) | 2024.02.02 |
| False Position Method 설명 (python 구현) (0) | 2024.02.02 |


