Lagrange Polynomial Interpolation 설명 (python 구현)
- 목차
2024.02.02 - [데이터 분석/최적화 알고리즘] - Fibonacci Search 설명 (python 구현)
Lagrange Polynomial Interpolation
서로 다른 점 n개를 지나는 가장 낮은 차수의 함수를 찾는 보간법
수식
서로 다른 점 n개를 지나는 가장 낮은 차수의 함수를 찾는 보간법
- $y= \left(\frac{x-x_1}{x_0-x_1} \right)y_0 + \left(\frac{x-x_0}{x_1-x_0} \right)y_1$
- $y= \left(\frac{(x-x_1)(x-x_2)}{(x_0-x_1)(x_0-x_2)} \right)y_0 + \left(\frac{(x-x_2)(x-x_0)}{(x_1-x_2)(x_1-x_0)} \right)y_1 + \left(\frac{(x-x_0)(x-x_1)}{(x_2-x_0)(x_2-x_1)} \right)y_2$
- ...
구현 소스 코드
def lagrange(x, *points):
assert len(points) >= 2, "You have to input at least 2 points."
demominators = [1 for _ in range(len(points))] # 분모
numerators = [1 for _ in range(len(points))] # 분자
xs = [point[0] for point in points] # xi
ys = [point[-1] for point in points] # yi
# 각 항의 분자, 분모 계산
for i in range(len(points)):
for j in range(len(points)):
if i != j:
demominators[i] *= (xs[i]-xs[j])
numerators[i] *= (x-xs[j])
result = 0
for demoniator, numerator, y in zip(demominators, numerators, ys):
result += numerator / demoniator * y
return result
예제
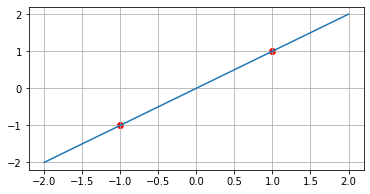
$(-1, -1)$과 $(1, 1)$을 지나는 함수
pts = [(-1, -1), (1, 1)]
def f(x):
return lagrange(x, *pts)
$(0,0)$, $(1, 1)$, $(-1, 1)$을 지나는 함수
pts = [(0, 0), (1, 1), (-1, 1)]
def g(x):
return lagrange(x, *pts)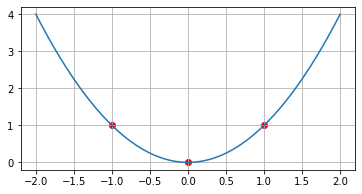
$(0, 0)$, $(1, 1)$, $(-1, -1)$, $(2, 8)$을 지나는 함수
pts = [(0, 0), (1, 1), (-1, -1), (2, 8)]
def h(x):
return lagrange(x, *pts)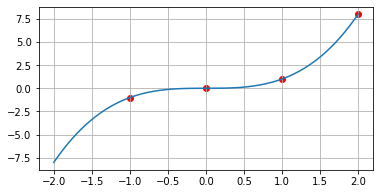
랜덤한 10개의 점을 지나는 함수
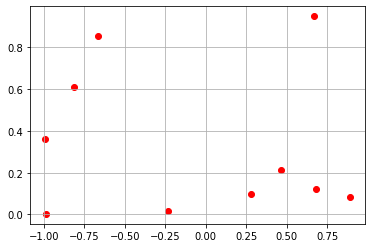
import random
x = [2*random.random()-1 for _ in range(10)]
y = [random.random() for _ in range(10)]
pts = list(zip(x, y))
def h(x):
return lagrange(x, *pts)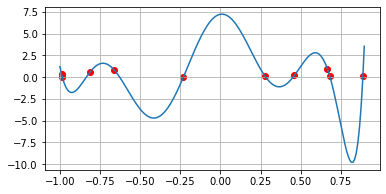
Lagrange를 이용한 Local Minimum 탐색
함수 $f(x)$가 최소가 되게 하는 $x$를 찾는 알고리즘
수식
1. $f'(a)f'(b)<0$인 구간 $[a, b]$ 설정 및 $c=(a+b)/2$
2. 점 $a$, $b$, $c$를 지나는 Lagrange polynomial 함수인 $\hat f$를 찾음
3. 이 함수의 local minimum을 만드는 점 $\theta$에 대해 $f'(\theta)$를 계산
- $f'(a)f'(\theta)<0$이면 $[a, \theta]$에 대해 반복, $f'(b)f'(\theta)<0$이면 $[\theta, b]$에 대해 반복
- $f'(\theta)=0$이면 $\theta$가 $f$의 local minimum
구현 소스 코드
class gss:
def __init__(self, a, b, func, tol=1e-6):
self.xl = a
self.xu = b
self.func = func
self.tol = tol
def solve(self):
a_history = [self.xl]
b_history = [self.xu]
phi = (1+5**0.5)/2
d = (phi-1)*(self.xu - self.xl)
x1 = self.xl+d
x2 = self.xu-d
while True:
# 허용범위 이내일 때
fxl = self.func(self.xl)
fxu = self.func(self.xu)
if fxl < fxu:
xopt = self.xl
else:
xopt = self.xu
epsilon = (2 - phi) * abs((self.xu-self.xl)/xopt)
if epsilon <= self.tol:
self.minimum = (self.xl + self.xu) / 2
self.history = [(a, b) for (a, b) in zip(a_history, b_history)]
return self.minimum
fx1 = self.func(x1)
fx2 = self.func(x2)
if fx1 < fx2:
self.xl = x2
x2 = x1
d = (phi-1)*(self.xu - self.xl)
x1 = self.xl+d
else:
self.xu = x1
x1 = x2
d = (phi-1)*(self.xu - self.xl)
x2 = self.xu-d
a_history.append(self.xl)
b_history.append(self.xu)
def derivative(func, x):
delta_x = 1e-4
fx_plus_delta = func(x + delta_x)
fx_minus_delta = func(x - delta_x)
return (fx_plus_delta - fx_minus_delta) / (2 * delta_x)
class lagrange_search:
def __init__(self, func, a, b, tol=1e-4):
assert derivative(func, a) * derivative(func, b) < 0, "f'(a) * f'(b) must be less than 0"
self.func = func
self.a = a
self.b = b
self.tol = tol
def solve(self):
a_history = [self.a]
b_history = [self.b]
while True:
pts = [(self.a, self.func(self.a)), (self.b, self.func(self.b)), ((self.a+self.b)/2, self.func((self.a+self.b)/2))]
fhat = lambda x:lagrange(x, *pts)
# 라그랑지 함수를 최소로 만드는 값은 golden section search로 해결
theta = gss(a=self.a, b=self.b, func=fhat).solve()
fprimea = derivative(self.func, self.a)
fprimeb = derivative(self.func, self.b)
fprimet = derivative(self.func, theta)
if (abs(fprimet) <= self.tol) or (abs(self.func(theta)) <= self.tol):
self.minimum = theta
self.history = [(a, b) for (a, b) in zip(a_history, b_history)]
return theta
elif fprimea * fprimet < 0:
self.b = theta
else:
self.a = theta
a_history.append(self.a)
b_history.append(self.b)
예제
$f(x) = \sin ({ \cos ({ \rm{e}^x }) })$
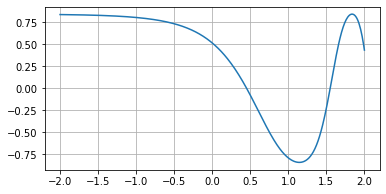
LS = lagrange_search(func=f, a=0, b=1.5)
LS.solve() # 1.144730643441196
f(LS.minimum) # -0.8414709848063662
$g(x) = x^3 - x$
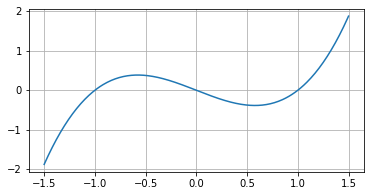
LS = lagrange_search(func=g, a=-0.5, b=2)
LS.solve() # 0.5773785954288917
g(LS.minimum) # -0.38490017806997207
전체 소스 코드 → github
'데이터 분석 > 최적화 알고리즘' 카테고리의 다른 글
| 유전 알고리즘 python 코드를 통해 알아보기 (0) | 2024.02.02 |
|---|---|
| 수치 최적화 알고리즘 정리 (0) | 2024.02.02 |
| Fibonacci Search 설명 (python 구현) (0) | 2024.02.02 |
| Newton's Method (Quadratic interpolation with 2nd derivative) 설명 (python 구현) (0) | 2024.02.02 |
| Golden Section Search 설명 (python 구현) (0) | 2024.02.02 |


