유전 알고리즘 python 코드를 통해 알아보기
- 목차
2024.01.31 - [데이터 분석/알고리즘] - 유전 알고리즘 간단 소개
유전 알고리즘 간단 소개에 이어서 이번엔 자세한 설명을 python 코드와 함께 진행하고자 한다.
0. 기본 배경
0-1. 목적
유전 알고리즘은 "최적해 탐색 알고리즘"이다. $y=f(x)$라는 함수가 있을 때, 어떤 $x$가 $y=0$으로 만드는 지를 알고 싶은 상황이 생길 수 있다. 이럴 때 사용하는 것이 "최적해 탐색 알고리즘"이며, 여기서 함수 $f$가 머신 러닝 등 수식적으로 파악할 수 없는(Blackbox) 모델인 경우를 "Blackbox Optimization", 통칭 BBO라고 부른다. 참고로 수식적으로 파악할 수 있는 모델은 수치 최적화 또는 최적해 탐색(root finding)이라고 부르며 다음 링크를 확인하자.
2024.02.02 - [데이터 분석/최적화 알고리즘] - 수치 최적화 알고리즘 정리
0-2. 필요한 라이브러리
- pandas
- numpy
- random, time (기본 내장 라이브러리)
0-3. Early Stopping
유전 알고리즘과는 관계 없지만 여기서는 사용되는 별도 클래스를 정의해주었다. tensorflow를 사용하는 사람에겐 익숙할 수도 있는 Early Stopping은 loss가 특정 횟수동안 감소하지 않으면 거기서 학습 혹은 탐색을 멈추도록 하는 기능을 갖고 있다.
class EarlyStopping:
def __init__(self, patience=5):
self.loss = np.inf
self.patience = 0
self.patience_limit = patience
def step(self, loss):
if self.loss > loss:
self.loss = loss
self.patience = 0
else:
self.patience += 1
def is_stop(self):
return self.patience >= self.patience_limit
1. 유전 알고리즘
python 코드와 함께 설명을 하도록 하겠다.
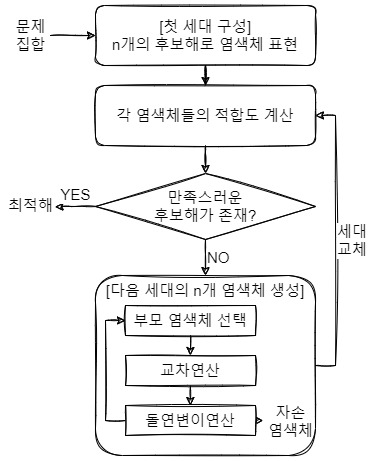
1-1. 랜덤 후보해 생성
def generate_feature(condition:dict, base:pd.Series, fix_features:dict) -> pd.Series:
"""
첫 세대의 각 데이터 생성
Parameters
----------
condition: 해의 범위
{'F1':{'mean':0, 'std':3, 'min':-100, 'max':100}, 'F2':{'mean':10, 'std':3, 'min':-100, 'max':50}}
* 필요시 condition2 = dataset.dtypes를 넣을 것 (해의 데이터 타입을 위함 int/float)
if condition2[col] == 'float64':
x = x
else:
x = int(x)
base: 생성 기준 (pd.Series)
fix_features: 고정시킬 features
{'F1':100, 'F2':50, ...}
Returns
-------
pd.Series
Examples
--------
condition = dataset.describe().to_dict()
base = dataset.iloc[-1]
fix_features = base[some_features].to_dict()
new_feature = generate_feature(condition, base, fix_features)
"""
indivisual = base.copy()
for col, value in condition.items():
if col in fix_features.keys():
indivisual[col] = fix_features[col]
continue
maximum = value['max']
minimum = value['min']
x = random.uniform(minimum, maximum)
indivisual[col] = np.round(x, 3)
return indivisual만족하는 최적해를 찾기 위해, 전체 피처 공간에서 후보해를 만들어낸다. 후보해를 만드는 방법은 다양할 수 있는데, 이 코드에서는 `random.uniform`을 통해 해당 피처의 최대, 최솟값 사이의 임의의 값을 랜덤하게 뽑아낸다. 필요에 따라 표준편차를 이용하여 정규분포 확률로부터 추출할 수도 있다. 또, docstring에 적어놓은대로 특정 피처는 int형으로 특정될 수 있기 때문에 상황에 따라 함수를 고쳐주어야 제대로 된 탐색을 할 수 있다.
- `condition`: 탐색할 $x$의 최대 최소를 지정하여 해당 범위 내에서만 탐색. 정규분포로 추출하려면 평균과 표준편차 정보를 주는 것이 좋다.
- `base`: 개체를 만들기 위한 파라미터로, 갖고 있던 데이터 중 아무거나 가져오면 된다.
- `fix_features`: $x$이긴 하지만 고정된 값을 주고 싶을 때 사용한다. 예를 들어, 월 정보가 포함된 데이터로 모델을 만들었을 때, 1월의 최적해를 찾고 싶은 상황에서 `{'month':1}`이라고 주는 형식이다.
이 함수에서 후보해들은 유전 알고리즘에서 "개체" 혹은 "염색체"라고 불리며 개체들이 모이면 "세대"라고 부른다. 그리고 개체의 각 인자값을 "유전자"라고 부른다.
def generate_population(size:int, condition:dict, base:pd.Series, fix_features:dict) -> list:
"""
첫 세대 생성.
Parameters
----------
size: 생성할 데이터의 개수
condition: 해의 범위
{'F1':{'mean':0, 'min':-100, 'max':100}, 'F2':{'mean':10, 'min':-100, 'max':50}}
base: 생성 기준 (pd.Series)
fix_features: 고정시킬 features
{'F1':100, 'F2':50, }
Returns
-------
list [pd.Series, pd.Series, ...]
Examples
--------
size = 100
condition = dataset.describe().to_dict()
base = dataset.iloc[-1]
fix_features = base[some_features].to_dict()
population = generate_population(size, condition, base, fix_features)
"""
population = []
for i in range(size):
indivisual = generate_feature(condition, base, fix_features)
population.append(indivisual)
return population`size`를 지정하여 세대의 인구수를 지정한다.
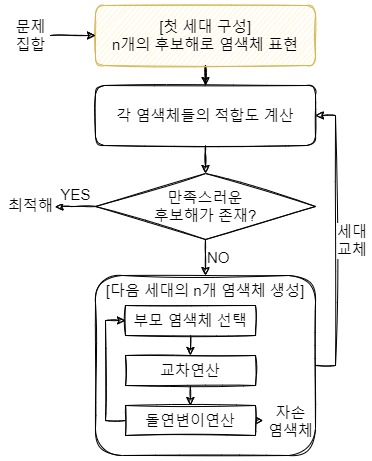
이것으로 첫 세대가 구성되었다.
1-2. 모든 후보해에 대해 적합도 계산
"적합도"라는 것은 쉽게 말해 후보해가 정답(최적해)에 얼마나 가까운지를 평가하는 것이다. 예를 들어 $f(x) = 10$이 되는 $x$를 찾으려고 할 때, 가장 쉽게 생각할 수 있는 적합도는 $f(x)$가 10에 가까울수록 낮은 loss를 갖도록 하는 $| f(x) - 10 |$이 될 것이다. (알고리즘 설계에 따라 loss가 아닌 score가 될 수 있고, 이 때는 높은 score를 갖도록 적합도를 설계해야 한다.)
def compute_performance(fitness, population:list) -> list:
"""
세대의 모든 데이터에 대해 loss 계산하여 오름차순 정렬
Parameters
----------
fitness: loss 계산식.
- input: indivisual(pd.Series)
- return: loss (float)
population: 세대 데이터 리스트
Returns
-------
list [(pd.Series, loss), (pd.Series, loss), ...]
Examples
--------
population = [test.iloc[0], test.iloc[1], test.iloc[2]]
population_sorted = compute_performance(fitness, population)
# [(test.iloc[2], 10), (test.iloc[0], 50), (test.iloc[1], 80)]
"""
performance_list = []
for indivisual in population:
loss = fitness(indivisual)
performance_list.append([indivisual, loss])
population_sorted = sorted(performance_list, key=lambda x:x[1], reverse=False)
return population_sorted문제 상황마다 적합도 함수는 계속해서 달라지기 때문에 사용자가 적합도 함수를 직접 입력하도록 설계했다. 그리고 가장 좋은 최적해가 list의 가장 앞에 있도록 loss 기준으로 오름차순 정렬을 해주었다.
- `fitness`: 적합도 함수. 아래와 같은 예시가 있을 수 있다.
# 학습이 완료된 모델을 `model`이라고 정의
def fitness(indivisual, model=model, goal=50):
pred = model.predict([indivisual])[0]
return abs(pred - goal)
- `population`: 세대 전체 데이터
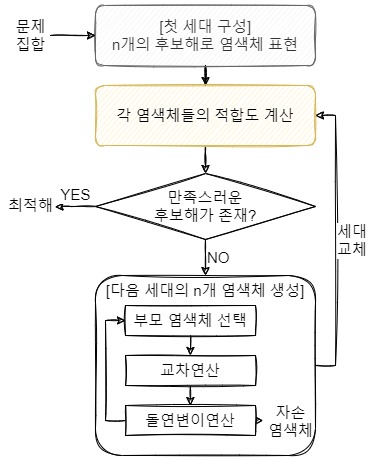
1-3. 다음 세대 생성
만족스러운 후보해가 없었다는 가정을 하고 다음 세대를 생성하는 과정을 보자.
부모 개체 선택
한 세대 내에서 살릴 부모를 선택하는 것이다. 자연 선택설처럼 가장 우수한 개체를 살리고 나머지는 죽이는 과정이다. 유전 알고리즘이 생물학적인 특성에서 만들어졌다는 걸 이 과정부터 확인할 수 있다. 선택하는 방식에는 대표적으로 3가지 방법이 있다.
- Elitism: 적합도가 높은 N개를 선택
- Roulette Wheel: 각 개체의 적합도를 확률로 사용하여 랜덤하게 선택
- Tournament: 세대를 N개로 균등 분리 후 그 안에서 Elitism/Roulette Wheel 적용하여 선택
여기서는 가장 단순한 Elitism 방식으로 진행을 하였다.
def select_survivors(population_sorted:list, best_sample:int, lucky_few:int) -> list:
"""
한 세대에서 살릴 데이터를 선택 (부모 데이터 선택)
Parameters
----------
population_sorted: loss가 낮은 순으로 정리된 세대 데이터
best_sample: loss가 낮은 `best_sample` 수만큼 다음 세대로 넘김
lucky_few: best_sample을 제외한 나머지 데이터 중 랜덤으로 `lucky_few` 만큼 다음 세대로 넘김
Returns
-------
list [pd.Series, pd.Series, ...]
Examples
--------
population_sorted = compute_performance(fitness, population)
# len(population) == 100
best_sample = 10
lucky_few = 10
parents = select_survivors(population_sorted, best_sample, lucky_few)
# len(parents) == 20
"""
# best_sample 수만큼 다음 세대로 보냄
parents = [population_sorted[i][0] for i in range(best_sample)]
# 랜덤으로 운이 좋은 부모들을 살림
lucky_survivors = random.sample(population_sorted[best_sample:], k=lucky_few)
for I in lucky_survivors:
parents.append(I[0])
# 다음 세대의 부모들을 섞음
random.shuffle(parents)
return parents- `population_sorted`: 이전 함수에서 loss 기준으로 정렬된 세대 데이터
- `best_sample`: 적합도가 높은 개체 수 지정
- `lucky_few`: 운 좋게 살아남은 개체 수 지정
여기서 '왜 적합도가 낮은 개체를 살릴까?'하는 의문이 생길 수 있다. 생물학적으로 접근한다면 운 좋게 살아남은 개체에게 좋은 유전자가 남아 있을 수 있기 때문이다. 수학적으로 바꿔 말하면 local minimum에 빠지는 상황을 방지하고자 함이다. 적합도가 높은 개체가 local minimum 근처에 있고 오히려 적합도가 낮았던 개체가 있는 곳이 global minimum인 상황이 있을 수 있다.
자식 개체 생성
살아남은 부모끼리 교배시켜 자식을 만드는 과정이다. 교배라는 용어 대신 교차(crossover)라고 하기도 한다. 두 개체를 선택해서 서로의 피처를 교차하는데 여러 방법이 있다.
- Probabilistic Gene Selection: 확률 모수 θ에 따라 결정
- Weighted Average: Weight 모수 θ로 계산된 가중 평균
- θ 결정 방법: 1/2 또는 부모 각각의 적합도를 계산 후 그 비율에 따라 결정
여기서는 θ 결정 방법(1/2 확률)으로 교차하였다.
def create_child(indivisual1:pd.Series, indivisual2:pd.Series) -> pd.Series:
"""
두 유전자를 교배하여 새로운 유전자 생성
Parameters
----------
indivisual1, indivisual2: 값을 섞을 두 데이터
Returns
-------
pd.Series
Examples
--------
indivisual1 = next_generation[0]
indivisual2 = next_generation[-1]
child = create_child(indivisual1, indivisual2)
"""
child = []
for i in range(len(indivisual1)):
if random.random() < 0.5: # 50% 확률로 1의 유전자 획득
child.append(indivisual1[i])
else: # 50% 확률로 2의 유전자 획득
child.append(indivisual2[i])
return pd.Series(child, index=indivisual1.index)
- `indivisual1`, `indivisual2`: 부모 개체
돌연변이 생성
앞서 부모를 선택할 때 운 좋게 살리는 부모 개체가 있었듯, 자식 세대에서도 돌연변이를 추가해 local minimum에서 벗어나고자 한다. 돌연변이가 오히려 자연에서 살아남는 걸 표현한다.
# 정규분포에 따라 노이즈 추가
def mutate_feature(indivisual:pd.Series, condition:dict, fix_features:dict) -> pd.Series:
"""
정규분포 확률에 따라 노이즈 추가
Parameters
----------
indivisual: 노이즈를 추가할 원본 데이터
condition: 해의 범위
{'F1':{'mean':0, 'min':-100, 'max':100}, 'F2':{'mean':10, 'min':-100, 'max':50}}
fix_features: 고정시킬 features
{'F1':100, 'F2':50, }
Returns
-------
pd.Series
Examples
--------
indivisual1 = next_generation[0]
indivisual2 = next_generation[-1]
child = create_child(indivisual1, indivisual2)
condition = dataset.describe().to_dict()
fix_features = base[some_features].to_dict()
mutated = mutate_feature(child, condition, fix_features)
"""
indivisual = indivisual.copy()
for i, (col, value) in enumerate(condition.items()):
if col in fix_features.keys():
indivisual[col] = fix_features[col]
continue
maximum = value['max']
minimum = value['min']
x = random.uniform(minimum, maximum)
indivisual[col] = np.round(x, 3)
return indivisual첫 개체를 만들 때와 거의 동일하게 최대-최소 사이에서 균등하게 랜덤 값을 추출한다. 상황에 따라 정규분포로 돌연변이를 만들 수도 있고, 확률에 따라 일부 유전자만 돌연변이를 줄 수도 있다.
자식 세대 생성
부모 선택 - 교배 - 돌연변이의 과정을 통해 자식 세대를 만든다. 만들어진 자식 세대를 가지고 다시 적합도 검사 및 선택-교배-돌연변이의 과정을 반복한다.
def create_children(parents:list, n_child:int, chance_of_mutation:int, condition:dict, fix_features:dict) -> list:
"""
교배, 변이 등을 통해 다음 세대 생성
Parameters
----------
parents: 한 세대에서 선택된 부모 데이터
n_child: 부모 한 쌍으로 만들어낼 자식 수
chance_of_mutation: 돌연변이를 만들 확률(%)
condition: 해의 범위
{'F1':{'mean':0, 'min':-100, 'max':100}, 'F2':{'mean':10, 'min':-100, 'max':50}}
fix_features: 고정시킬 features
{'F1':100, 'F2':50, }
Returns
-------
list [pd.Series, pd.Series, ...]
Examples
--------
parents = select_survivors(population_sorted, best_sample, lucky_few) # len(parents) == 20
n_child = 10
chance_of_muation = 10
condition = dataset.describe().to_dict()
fix_features = base[some_features].to_dict()
next_generation = create_children(parents, n_child, chance_of_mutation, condition, fix_features)
# len(next_generation) == 100 <=> (len(parents)// 2) * n_child == 100
"""
# chance_of_mutaion 만큼 돌연변이 생성
next_population = []
for i in range(len(parents)//2):
for j in range(n_child):
child = create_child(parents[i], parents[-i-1])
if random.random() * 100 < chance_of_mutation:
child = mutate_feature(child, condition, fix_features)
next_population.append(child)
return next_population- `parents`: 부모 세대
- `n_child`: 각 부모에게서 만들어낼 자식 수
- `chance_of_mutation`: 돌연변이를 만들어낼 확률
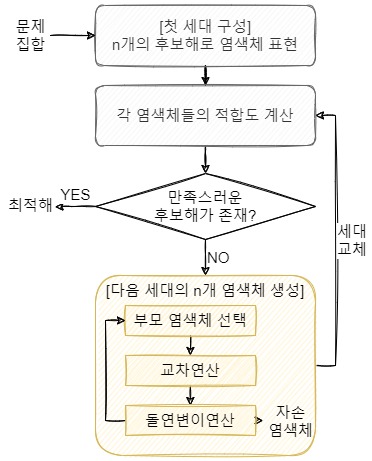
1-4. 반복 종료 조건
반복 종료는 아래 상황들로 정할 수 있다.
- 연속된 N세대 동안 loss가 감소하지 않았을 경우 (Early Stopping)
- 특정 탐색 시간을 초과한 경우
- 후보해 중 만족스러운 개체가 있는 경우
예를 들어 적합도 함수를 거쳤을 때 loss가 허용범위에 들어오면 반복을 끝내는 것이다.
pop_sorted = compute_performance(fitness, population=pop)
# 가장 loss가 낮은 데이터 확인
es.step(pop_sorted[0][1])
if es.is_stop(): # EarlyStopping 횟수만큼 loss 개선이 없으면 stop
break
if pop_sorted[0][1] < self.loss: # 이전 loss보다 좋아지면 저장
self.best = pop_sorted[0][0]
self.loss = pop_sorted[0][1]
if self.loss <= tolerance: # 차이가 허용범위 이하면 완료
break
2. 예시
상황을 가정하면, 자전거 대여 업체에서 수요 예측을 하는데, 1월의 수요가 400번일 때의 조건들(기상 상황과 시간대 등)을 알아내 자전거를 미리 정비하고자 한다.
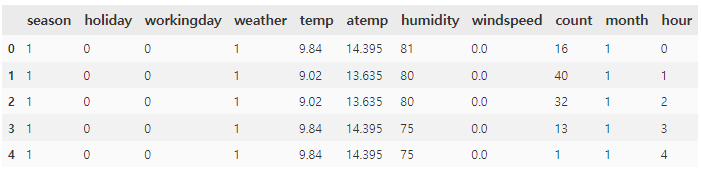
우선 수요 예측 모델을 만들어야 하므로 나는 간단하게 XGBoost 모델을 만들었다. 여기서 모델은 현실을 매우 잘 맞춘다고 가정하자. 그럼 이 모델에 어떤 데이터를 넣어야 400이라는 값을 뱉는지 유전 알고리즘을 통해 찾아내보자.
from genetic_algorithm import GeneticAlgorithm
ga = GeneticAlgorithm()먼저 유전 알고리즘 클래스를 호출한다.
def fitness(indivisual, model, goal):
pred = model.predict([indivisual])[0]
return abs(pred-goal)
condition = X_features[X_features['month']==1].describe().to_dict()
n_generation = 300
population = 100
best_sample = 20
lucky_few = 20
n_child = 5
chance_of_mutation = 10
fix_features = {'month':1}
base = X_features.iloc[0]
goal = 400
tolerance = 5
유전 알고리즘에 사용할 조건들을 설정한다. 여기서 1월의 수요 예측을 원하기 때문에 `condition`을 1월의 데이터 조건으로 한정하고, `fix_features= {'month':1}`로 지정한다. 목표값은 `goal = 400`이며 loss가 `tolerance = 5` 이하로 내려가면 반복을 종료한다.
best = ga.search(
condition=condition,
fitness=lambda x:fitness(x, xgb, goal),
n_generation=n_generation,
population=population,
best_sample=best_sample,
lucky_few=lucky_few,
n_child=n_child,
chance_of_mutation=chance_of_mutation,
fix_features=fix_features,
tolerance=tolerance,
base=base,
es=None,
verbose=True,
time_limit=None,
)Early Stopping은 별도로 설정하지 않았다. 주의해서 볼 부분은 fitness에 모델과 목표를 이렇게 넣어줘야 한다는 점이다. 실행하면 매우 순식간에 값을 찾아낸다.

실제로 값을 예측해보자.

그럼 어떤 조건들일 때 저 값을 예측하는지도 확인해보자.
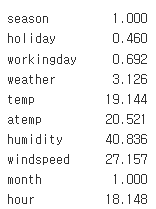
잘 찾아낸 것 같지만 실제로는 holiday 등 일부 값들은 int형이기 때문에 보정이 필요하다.
3. 유전 알고리즘의 장단점
장점
- 좋은 해 끼리 결합하여 더 좋은 해 발견 가능성
- 돌연변이를 통해 local minimum에서 빠져나올 수 있음
단점
- 일반적인 방법이 없음 (문제 상황에 따라 새로 정의할 필요가 있음)
- 최초 세대를 만들어줘야 함
- 랜덤성의 영향을 많이 받음
- 예측 모델이 정확하지 않으면 찾아낸 최적해가 현실에서 정답이라고 장담할 수 없다.
전체 소스 코드
참조
[ Genetic Algorithm ] 유전 알고리즘을 통해 비밀번호를 뚫어보자! — 수구리의 데브로그 (tistory.com)
'데이터 분석 > 최적화 알고리즘' 카테고리의 다른 글
| Nelder-Mead Method 간단 소개 (0) | 2024.02.03 |
|---|---|
| Differential Evolution 간단 소개 (0) | 2024.02.02 |
| 수치 최적화 알고리즘 정리 (0) | 2024.02.02 |
| Lagrange Polynomial Interpolation 설명 (python 구현) (0) | 2024.02.02 |
| Fibonacci Search 설명 (python 구현) (0) | 2024.02.02 |


