선형회귀로 시계열 예측 모델 만들 때 조심할 점
- 목차
1. 데이터 선정
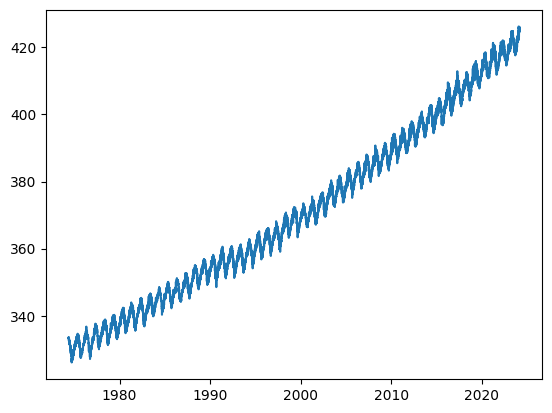
데이터 수도 많고 트렌드와 주기성도 매우 잘 보이는 Mauna Loa CO2 daily means 데이터를 이용하였다.
Global Monitoring Laboratory - Carbon Cycle Greenhouse Gases (noaa.gov)
2. 데이터 전처리
선형적으로 증가하는 트렌드도 보이고 1년 주기로 증감을 반복하는 패턴이 보인다. 트렌드와 패턴을 고려한 x인자를 만들자.
$y = c_0 + c_1 x + c_2 x^2 + c_3 x^3 + c_4 \sin(\frac{2\pi x} {T}) + c_5 \cos(\frac{2\pi x} {T}) + c_6 \sin(\frac{4\pi x} {T}) + c_7 \cos(\frac{4\pi x} {T}) \text{ where } T=1\text{ year}$
$ \sin(\frac{4\pi x} {T})$ 항과 $\cos(\frac{4\pi x} {T})$ 항은 굳이 필요한가 싶긴 하지만 일단 넣어서 진행했다.
def make_dataset(X, y, T):
df = pd.DataFrame(X, columns=['X'])
df['X2'] = X ** 2
df['X3'] = X ** 3
df['cosX'] = np.cos(2*np.pi*X/T)
df['sinX'] = np.sin(2*np.pi*X/T)
df['cos2X'] = np.cos(2*np.pi*2*X/T)
df['sin2X'] = np.sin(2*np.pi*2*X/T)
df['y'] = y
return df
3. 일반적인 선형 회귀
일 데이터이므로 x 값을 0, 1, 2, ...로 순차적으로 증가하도록 설정해서 선형 회귀에 적합해보자.
from sklearn.linear_model import LinearRegression
df_index = make_dataset(np.arange(0, len(df)), df['데이터'], T=365.25) # 1년=365.25일
Xs = ['X', 'X2', 'X3', 'cosX', 'sinX', 'cos2X', 'sin2X']
lr = LinearRegression().fit(df_index[Xs], df_index['y'])
prd_idx = lr.predict(df_index[Xs])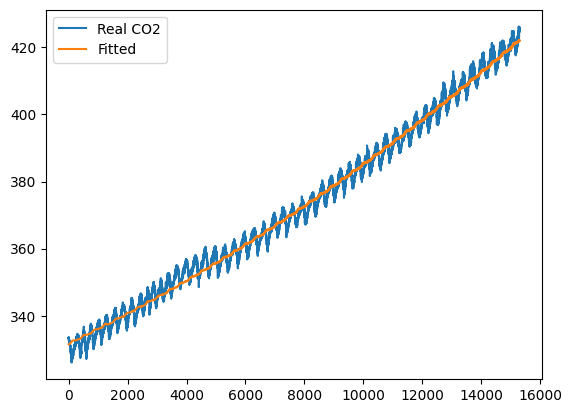
트렌드는 맞는 것처럼 보이는데 패턴을 전혀 맞추지 못하는 모습을 보인다.
4. 날짜를 값으로 변경 후 선형 회귀
값으로 변경한다는 건 2024년 1월 1일을 2024.0으로, 2024년 12월 31일을 2024.99로 보는 것이다. 이렇게 하면 윤달도 자동으로 고려되며, 혹여 있을 빠진 날짜까지 고려된다.
def datetime_to_float(d):
start_of_year = pd.Timestamp(year=d.year, month=1, day=1)
end_of_year = pd.Timestamp(year=d.year+1, month=1, day=1) - pd.Timedelta(days=1)
total_days = (end_of_year - start_of_year).days + 1
elapsed_days = (d - start_of_year).days
return d.year + elapsed_days / total_days
from sklearn.linear_model import LinearRegression
df['X'] = pd.to_datetime(df['년'].astype(str) + '-' + df['월'].astype(str) + '-' + df['일'].astype(str)).apply(datetime_to_float)
df_time = make_dataset(df['X'], df['데이터'], T=1) # 주기 1년
lr = LinearRegression().fit(df_time[Xs], df_time['y'])
prd = lr.predict(df_time[Xs])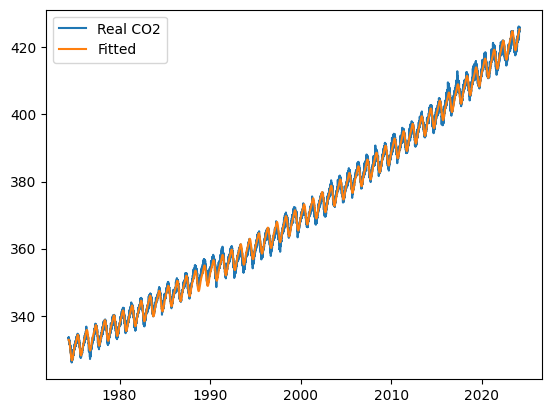
잘 맞는 모습을 보인다.
5. 미래 예측
위에서 적합한 선형 회귀 모델로 미래 값을 예측해보자.
prd_times = pd.Series(pd.date_range(start='2024-3-12', end='2030-12-31', freq='D')).apply(datetime_to_float)
df_prd = make_dataset(prd_times, 0, T=1)
prd = lr.predict(df_prd[Xs])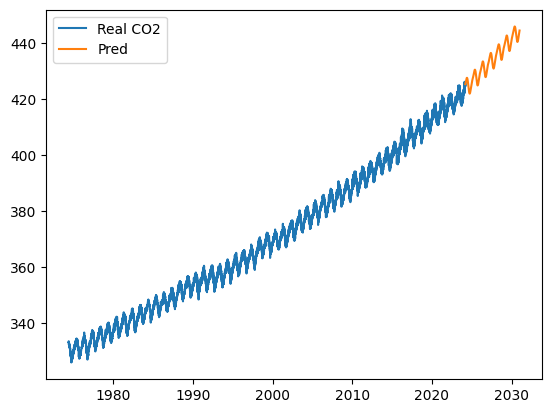
교훈: 선형 회귀로 시계열을 적합할 때는 X를 정수 인덱스를 사용하지 말고 시간을 백분율로 바꾼 값을 쓰도록 하자.
6. 전체 코드
'데이터 분석 > 머신러닝' 카테고리의 다른 글
| 분류 모델의 shap value를 확률값으로 확인하기 (0) | 2024.05.27 |
|---|---|
| shap 명목형 변수 표기 방법 바꾸기 (0) | 2024.05.21 |
| AutoML, Autogluon vs mljar-supervised (0) | 2024.02.29 |
| Regression - IBUG 알고리즘 논문 읽기 (0) | 2024.02.27 |
| 상관 관계의 종류 및 python 코드 구현 (0) | 2024.02.19 |



